Es gibt immer wieder Situationen, wo man Einheiten umrechnen muss. Dabei sind die gängigsten Einheiten wie Meter in Zentimeter umzurechnen ja noch überschaubar, aber wie rechnet man beispielsweise die Einheit Liter pro Quadrat Sekunde in Kubikmeter pro Stunde um?.
Als erstes sollte man sich die grundlegenden physikalischen Einheiten und ihre Größen in Erinnerung rufen. Alle physikalischen Größen werden immer als Potenzprodukte der 7 Basisgrößen (Länge, Masse, Zeit, elektrische Stromstärke, Temperatur, Stoffmenge und Lichtstärke) dargestellt. Dieses Potenzprodukt bezeichnet man als Dimension der jeweiligen Größe. Sie darf nicht mit der Einheit der Größe verwechselt werden und ist unabhängig vom Maßsystem.
| Einheit | Zeichen | Größe | Einheit | Zeichen | Größe |
| Dezi | d | Deka | da | ||
| Zenti | c | Hekto | h | ||
| Milli | m | Kilo | k | ||
| Micro | µ | Mega | M | ||
| Nano | n | Giga | G | ||
| Piko | p | Tera | T | ||
| Femto | f | Peta | P | ||
| Atto | a | Exa | E | ||
| Zepto | z | Zetta | Z | ||
| Yokto | y | Yota | Y |
Um Größen entsprechend umrechnen oder konvertieren zu können, ist neben dem Maßsystem auch gut, wenn man bestimmte weitere Zusammenhänge kennt, die sich nicht zwingend als Potenz-Produkte ableiten lassen. Einige dieser Zusammenhänge sind in der folgenden Tabelle aufgeführt (ohne Anspruch auf Vollständigkeit:
| Zeit [t] | Basiseinheit ist die Sekunde [s] 60 s = 1 min (Minute) 60 min = 1 h (Stunde) = 3600 s 24 h = 1 Tag = 1440 min = 86400 s |
| Liter [l] | Basiseinheit ist der Liter [l] 1 Liter = 1 1 |
| Fläche [A] | Basiseinheit ist der Quadratmeter 1 Ar = 100 1 HAr = 100 Ar = |
| Arbeit [W] | Basiseinheit ist das Joule [J] 1 J = 1 Nm = 1 kg |
| Leistung [P] | Basiseinheit ist das Watt [W] 1 W = 1 kg |
| Masse [m] | Basiseinheit ist das Kilogramm [kg] 1 Tonne [t] = 1 000 kg |
Umrechnungsbeispiele
Beispiel 1
Es sollen
(1) ![]()
umgerechnet werden.
Schritt1: Konvertierung der Einheiten mit Basiswissen:
1 ![]() = 1000 Liter daraus folgt 1 l =
= 1000 Liter daraus folgt 1 l = ![]()
1 h = 3600 s daraus folgt 1s = ![]()
Eingesetzt ergibt sich dann:
(2) 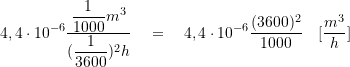
Rechnet man dann weiter ergibt sich :
(3) ![]()
Beispiel 2
Wieviel sind 122 cm/min umgerechnet km/h ?
Auch hier geht man wieder so vor, dass man die gegebenen Einheiten in Bezug zu den gesuchten Einheiten setzt. Also 1km = 1000 m, 1m = 100 cm damit entspricht 1 km = 1000 * 100 cm = ![]() cm oder 1 cm =
cm oder 1 cm = ![]() .
.
Analog dazu verfährt man mit der zweiten Größe: 1h = 60 min damit entspricht 1 min = ![]() . Diese Werte werden nun wieder in die EInheitengleichung eingesetzt:
. Diese Werte werden nun wieder in die EInheitengleichung eingesetzt:
(4) ![]()