Bei der Kurvendiskussion geht es darum, eine mathematische Funktion zu untersuchen. D.h. das Verhalten zu verstehen. Dazu gibt es eine Menge von Eigenschaften, die von besonderem Interesse sind. Beispielsweise sind die Extremwerte von Interesse. Aber es gibt noch andere Aspekte, die man betrachtet (oder diskutiert). Dazu zählen üblicherweise folgende Eigenschaften:
- Definitionsmenge
- Nullstellen
- Schnittpunkte mit der Y-Achse
- Symmetrie Verhalten (Punkt- oder Achsen-Symetrie)
- Verhalten im Unendlichen (Grenzwert-Betrachtungen)
- Extremwerte (Hoch- und Tief-Punkte)
- Wendepunkte
- Graph der Funktion
- Monotonie Betrachtung (Steigend oder Fallend)
- Krümmungsverhalten
- Wertemenge
Wie man diese Eigenschaften bestimmen kann und anhand welcher Kriterien man das Verhalten dann beschreibt, erfolgt immer nach dem gleichen Schema. Und durch Anwendung verschiedener mathematischen Methoden. Beispielsweise die Bestimmung der Ableitung, das Integrieren oder das Lösen von Gleichungen. Daher bietet sich dieses Thema sehr gut an für Tests. und Prüfungen.
Im folgenden Beitrag wird an einem Beispiel eine vollständige Kurvendiskussion durchgeführt und beispielhaft die Methodik erklärt, die sich dann auf beliebte andere Funktionen übertragen lässt. Das Beispiel soll folgende Funktion sein:
![]()
Die Definitionsmenge
Die Definitionsmenge gibt an, welche Werte (Zahlen) man in die Funktion (für das x) einsetzen darf. Alle diese Zahlen, die man für x einsetzen darf, sind dann die Definitionsmenge.
Den Definitionsbereich einer Funktion oder eines Terms bestimmt man, indem man untersucht, ob einzelne Teile des (Funktions)terms für bestimmte Zahlenbereiche nicht definiert sind. Zahlen aus diesen Bereichen muss man aus der Definitionsmenge herausnehmen.
In unserem Beispiel finden wir keine Einschränkungen, somit kann die Definitionsmenge wie folgt angegeben werden:
![]()
Bestimmung der Nullstellen
Die Nullstellen einer Funktion f(x) sind die Stellen an denen f(x)=0 gilt. Oder geometrisch gesehen die Schnittpunkte des Graphen der Funktion f(x) mit der x-Achse.
D.h. man bestimmt die Nullstellen einer Funktion dadurch das man sie gleich Null setzt und durch verschiedenste Verfahren, dann die x-Werte bestimmt, an denen die Bedingung erfüllt ist. Mögliche Verfahren sind hier die Mitternachtsformel, das Horner-Schema oder auch die Linearfaktor-Zerlegung. Manchmal muss man einfach auch mal durch systematisches Probieren eine erste Nullstelle ermitteln, um dann weiter zu rechnen.
In unserem Beispiel kann man wie folgt vorgehen:
1. Nullstelle durch Probieren:
![]()
2. Nullstelle: Linerafaktor-Abspaltung über das Horner-Schema
Daraus ergibt sich dann folgende Darstellung:
![]()
Somit erhalten wir eine dreifache Nullstelle und eine weitere vierte Nullstelle:
![]()
Schnittpunkte mit der Y-Achse
Die Schnittstelle mit der y–Achse ist der Punkt wo der Graph die y–Achse schneidet. Der x-Wert, an dem die Funktion die y–Achse schneidet, ist immer null.
Daher lässt sich der y-Wert genau dadurch bestimmen, in dem der Wert x=0 in die Funktionsgleichung eingesetzt wird.
Bitte nicht mit der Bestimmung der Nullstelle verwechseln, wo der Wert y=0 gesetzt wird.
In unserem Beispiel setzten wir also x=0 in f ein und bestimmen somit f(0):
![]()
Symetrie
Man unterscheidet zwei Arten von Symmetrie: Punktsymmetrie und Achsensymmetrie. Eine Funktion ist punktsymmetrisch, wenn es irgendeinen Punkt gibt, an dem man die Funktion derart spiegeln kann, dass als Spiegelbild wieder die gleiche Funktion rauskommt.
Eine Funktion ist dagegen achsensymmetrisch, wenn es eine Gerade [also eine Achse] gibt, an der man die Funktion derart spiegeln kann, dass als Spiegelbild wieder die gleiche Funktion rauskommt.
Um herauszufinden ob eine Funktion symmetrisch ist gibt es zwei Formeln:
Wenn f(-x) = f(x) gilt, liegt eine Achsensymmetrie zur Y-Achse vor.
Wenn f(-x) = -f(x) gilt, liegt eine Punktsymetrie zum Ursprung vor.
Es gibt allerdings auch bei der Symmetrie-Untersuchung ganzrationalen Funktionen einen Trick. Bei dieser Art von Funktionen schaut man sich nur die Hochzahlen der Variablen an.
Gibt es nur gerade Hochzahlen, ist f(x) symmetrisch zur y-Achse.
Beispiele: f(x) = 2x6–3x4–5
Gibt es nur ungerade Hochzahlen, ist f(x) symmetrisch zum Ursprung.
Beispiele: f(x) = 2x5+12x3–2x f(x) = 2x-1+x-3–3²x-5+ x³–4x
Gibt es gemischte Hochzahlen, ist f(x) nicht symmetrisch.
Beispiele: f(x) = x3+2x2–3x+4 f(x) = 2x·(x³+6x²+9x)
In unserem Beispiel handelt es sich um Polynom mit gemischten Hochzahlen, woraus wir ableiten können, dass keine Symmetrie vorliegt.

Verhalten im Unendlichen
Bei dieser Untersuchung prüft man wie sich die Funktion verhält, wenn die X-Werte gegen plus oder minus Unendlich gehen. Dabei kommt es immer auf den Faktor mit der größten Hochzahl an, da dieser das Verhalten am stärksten beeinflusst.
In unserem Beispiel wäre das der Faktor ![]() . Möchte man nun wissen, wie das Verhalten im Unendlichen aussieht, setzt man gedanklich eine ganz große negative und eine positive Zahl ein und erkennt, dass durch die geradzahlige Hochzahl in beiden Fällen
. Möchte man nun wissen, wie das Verhalten im Unendlichen aussieht, setzt man gedanklich eine ganz große negative und eine positive Zahl ein und erkennt, dass durch die geradzahlige Hochzahl in beiden Fällen ![]() strebt.
strebt.
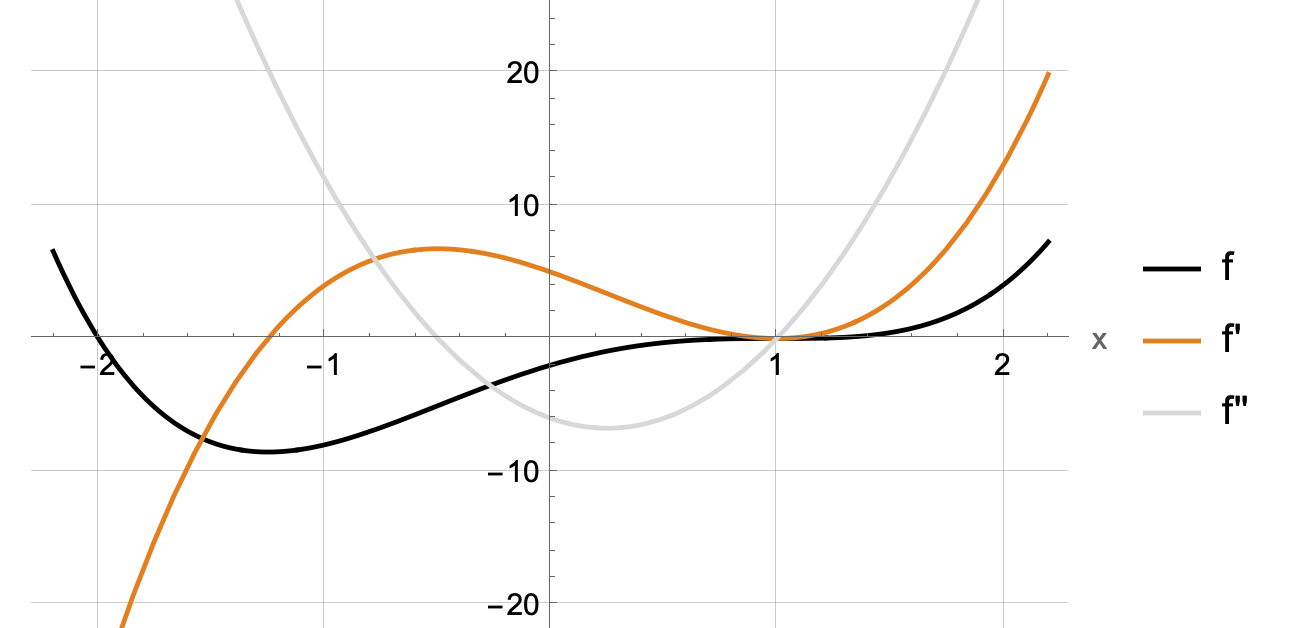
Extremwerte
Die Bestimmung der Extremwerte gehört zu den wichtigsten Untersuchungen. Als Extremwerte werden die Hochpunkte, Tiefpunkte und Sattelpunkte einer Funktion bezeichnet. Die Berechnung erfolgt immer nach dem geglichen Schema:
- Ist f'(x) = 0 so liegt ein Extremwert xe vor.
um was für einen Extremwert es sich handelt ergibt die zweite Ableitung: - Ist f“(xe) < 0 liegt ein Hochpunkt vor.
- Ist f“(xe) > 0 liegt ein Tiefpunkt vor.
- Ist f“(xe) = 0 steht Überprüfung für Sattelpunkt / Wendepunkt an.
Um also die Extremwerte zu bestimmen, müssen die Ableitungen berechnet werden:
![]()
![]()
![]()
Dann müssen die Nullstellen der ersten Ableitung berechnet werden: ![]()
In dem diese Nullstellen als x-Werte in die zweiten Ableitungen eingesetzt werden erhält man:
![]()
So erhält man die Funktionswerte über die dann, auf Grund der obigen Kriterien, ersichtlich wird um welche Art von Extremwert es sich an den berechneten Stellen handelt. In unserem Beispiel haben wir bei ![]() einen Tiefpunkt (weil der Funktionswert f“> 0 ist. Und am Punkt
einen Tiefpunkt (weil der Funktionswert f“> 0 ist. Und am Punkt ![]() steht eine weitere Untersuchung auf mögliche Wendepunkte an, da so noch keine Aussage gemacht werden kann.
steht eine weitere Untersuchung auf mögliche Wendepunkte an, da so noch keine Aussage gemacht werden kann.
![]()
Wendepunkte
Ein Wendepunkt einer Funktion ist der Punkt, an dem der Funktionsgraph sein Krümmungsverhalten verändert. D.h. an diesem Punkt wechselt der Graph entweder von einer Rechts- in eine Linkskurve oder anders herum. Ein Wendepunkt liegt vor, wenn gilt: f’’(x) = 0 und f’’’(x) ≠ 0.
In unserem Beispiel müssen wir die Nullstellen der 2. Ableitung bestimmen, und benötigen dann noch die 3. Ableitung von f(x) um herauszufinden on ein Wendepunkt vorliegt.
![]()
![]()
Somit erhalten wir durch Einsetzen der gefundenen Nullstellen der zweiten Ableitung für ![]() und
und ![]() woraus wir erkennen, dass an beiden Punkten ein Wendepunkt vorliegt, da das oben genannte Kriterium f’’(x) = 0 und f’’’(x) ≠ 0 erfüllt ist. Wir halten somit fest:
woraus wir erkennen, dass an beiden Punkten ein Wendepunkt vorliegt, da das oben genannte Kriterium f’’(x) = 0 und f’’’(x) ≠ 0 erfüllt ist. Wir halten somit fest:
![]()
Der Graph der Funktion zeichnen
Um den Graph zu zeichnen erstellt man sich am einfachsten eine Wertetabelle beispielsweise von [-3 bis 3] in einem passenden Abstand. Unter Berücksichtigung der bereits ermittelten Werte kann man dann recht schnell in passender Genauigkeit den Graphen zeichnen.
Wertetabelle { x, f(x) }
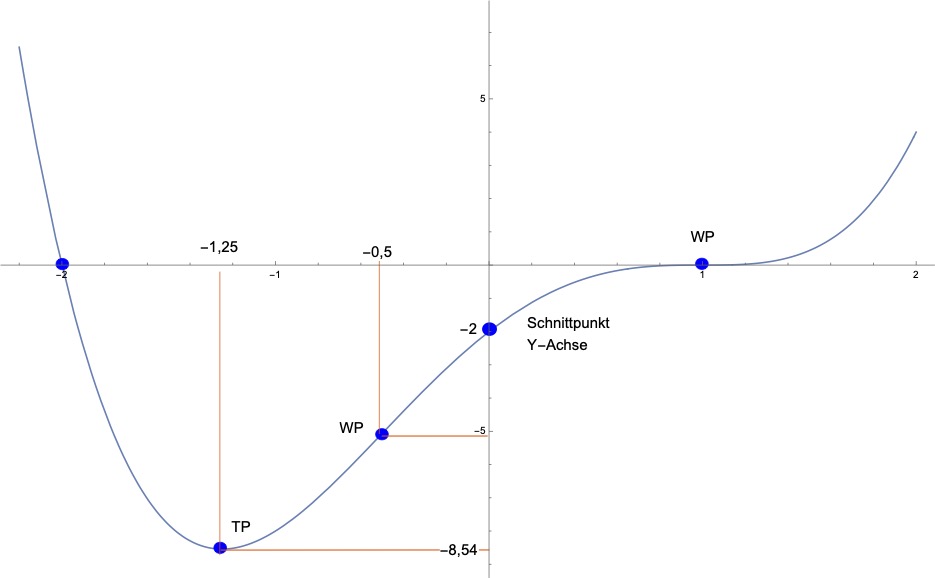
{-3.0, 64}, {-2.5, 21.43 }, {-2,0}, {-1.5, -7.8 }, {-1., -8.}, {-0.5, -5.1 }, {0, -2.0}, {0.5, -0.31}, {1, 0}, {1.5, 0.4}, {2.0, 4.0}, {2.5, 15.2}, {3.0,40}
Der Graph der Funktion sieht dann wie folgt aus:
Monotonie Verhalten
Das Monotonieverhalten einer Funktion gibt an, in welchem Bereich der Graph der Funktion steigt oder fällt. Daher ist das Monotonieverhalten wie folgt definiert: Die Funktion f ist streng monoton steigend, wenn f'(x) > 0 gilt. Die Funktion f ist streng monoton fallend, wenn f'(x) < 0 gilt.
Wichtig ist hierbei, dass Monotonie nur für die Teile des Definitionsbereiches betrachtet wird, in dem die Funktion stetig ist. Wenn bei einer Funktion Unterbrechungen existieren gibt es an diesen Stellen keine Monotonie. Daher ist es wichtig den Definitionsbereich der Funktion zu kennen.
In unserem Beispiel ist ![]() die in orange eingezeichnete Kurve. Um das Monotonie Verhalten von f(x) (der schwarz eingezeichneten Kurve) zu bestimmen, erstellt man am einfachsten eine Wertetabelle und zeichnet beide Funktionen in ein Diagramm.
die in orange eingezeichnete Kurve. Um das Monotonie Verhalten von f(x) (der schwarz eingezeichneten Kurve) zu bestimmen, erstellt man am einfachsten eine Wertetabelle und zeichnet beide Funktionen in ein Diagramm.
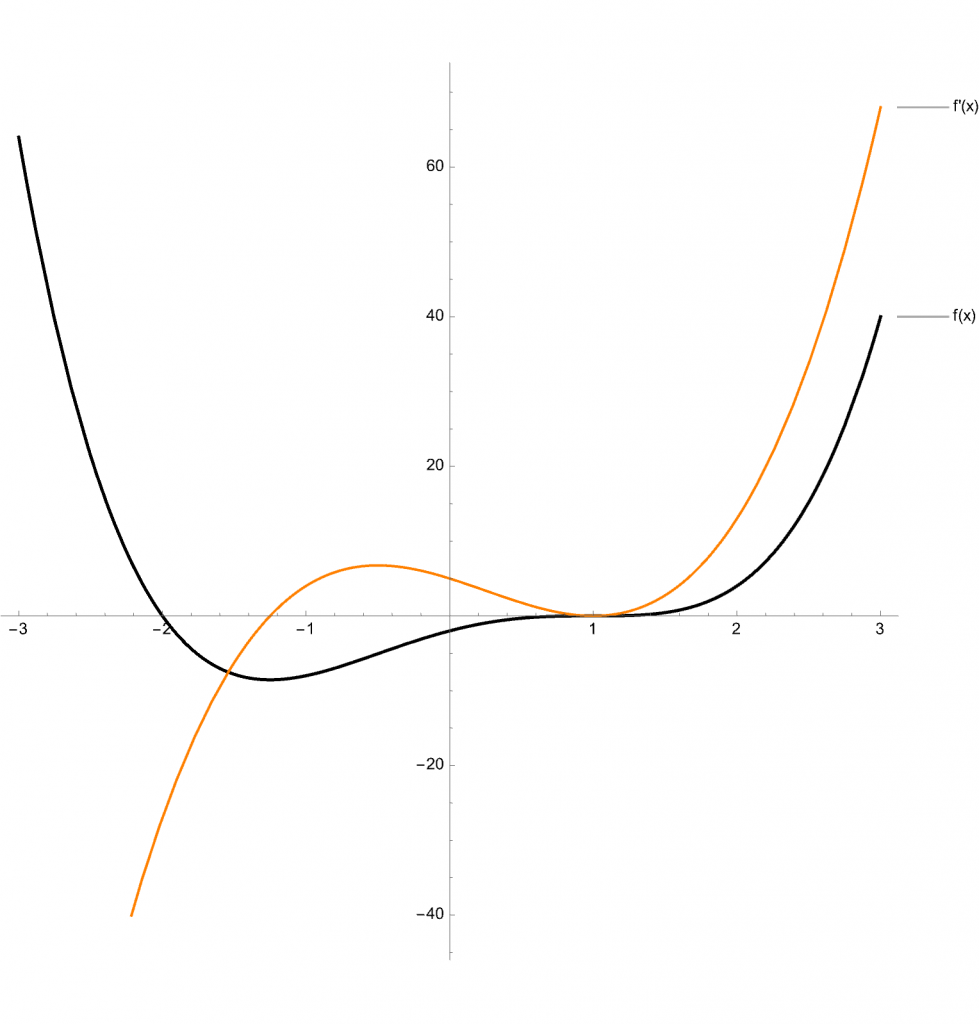
Man erkennt am Verlauf sehr gut, in welchen Bereichen der Wert von f'(x) kleiner Null ist und somit deutlich wird, dass f(x) monoton fallend ist. Im obigen Beispiel ist f´(x) im Intervall ![]() kleiner Null, somit hat die Ausgangsfunktion f(x) hier ein monoton fallendes Verhalten. Was man am Verlauf des Graphen (in schwarz dargestellt) sehr gut erkennen kann.
kleiner Null, somit hat die Ausgangsfunktion f(x) hier ein monoton fallendes Verhalten. Was man am Verlauf des Graphen (in schwarz dargestellt) sehr gut erkennen kann.
Ebenso erkennt man, wo der Wert von f'(x) größer Null ist, was gleichbedeutend damit ist, dass die Ausgangsfunktion f(x) monoton steigend ist.
Krümmungsverhalten
Beim Krümmungsverhalten in der Mathematik untersucht man, ob eine Funktion linksgekrümmt oder rechtsgekrümmt ist. In manchmal Fällen kann eine Funktion beide Krümmungen aufweisen. Die Untersuchung kann über die zweite Ableitung durchgeführt werden.
Bei der Rechtskrümmung ist die zweite Ableitung an der Stelle x kleiner Null: f“(x) < 0.
Die Rechtskrümmung wird auch als konkav bezeichnet.
Bei der Linkskrümmung ist die zweite Ableitung an der Stelle x größer als Null: f“(x) > 0.
Die Linkskrümmung wird auch als konvex bezeichnet.
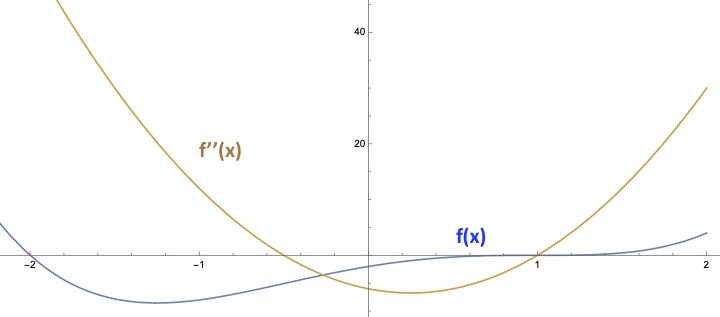
Dazu zeichnet man sich am einfachsten die 2. Ableitung zusammen mit dem Funktionsgraphen in ein Diagramm, um dadurch ablesen zu können, wie sich die Krümmung verhält. Im obigen Beispiel erkennt man, dass die 2. Ableitung zwischen den beiden Nullstellen negativ ist d.h. eine Rechtskrümmung vorliegt, in allen anderen Bereichen dagegen positiv und somit eine Linkskrümmung aufweist.
Wertemenge
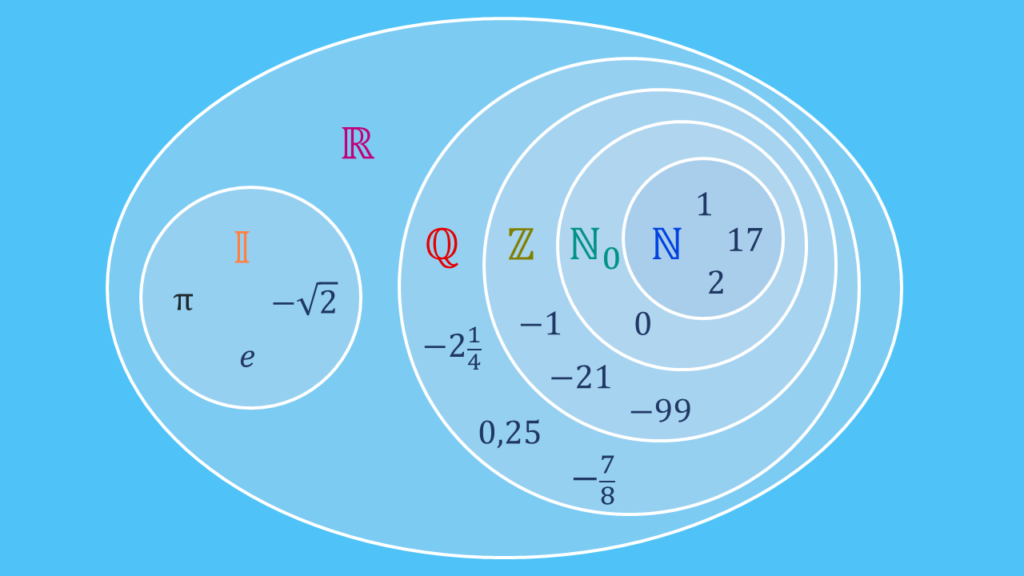
Die Wertemenge gibt an, welche Werte für f(x) rauskommen können, wenn man jede Zahl aus der Definitionsmenge in die Funktion (als x-Werte) eingesetzt hat. Hier muss man also auf Wissen über die Zahlenmengen (Ganze Zahlen, Natürliche Zahlen, etc) zurück greifen.
In unserem Beispiel entspricht der Wertebereich der Menge der Reellen Zahlen. Geschrieben in Menegenschreibweise sieht das Ergebnis dann so aus:
![]()
Zur Erinnerung man kennt in der Mathematik folgende Zahlenmengen:

Jede Zahlenmenge schließt die vorherigen Zahlen mit ein. So gehören zu den reellen Zahlen die natürlichen, ganzen, rationalen und auch irrationalen Zahlen. Es gilt demnach: