Veranschaulichung der Ableitung einer Funktion

Viele Schüler und Studenten tun sich etwas schwer, wenn es darum geht sich die Ableitung einer Funktion vorzustellen. Sie können zwar häufig durch die Anwendung der Ableitungsregeln, die Funktion ableiten, oft ist es aber mehr als nur hilfreich, wenn man auch versteht, was sich hinter dieser elementaren Operation verbirgt. Im folgenden soll mit Hilfe von Mathematica vorgestellt werden, wie die Ableitung-Operation visualisiert werden kann.

Ableiten heisst die Steigung eines Punktes P auf einem Graphen G zu bestimmen. Man lernt auch, dass man sich diesen Vorgang durch Anlegen einer Tangente an diesen Punkt vorstellen kann.

Um das Vorstellungsproblem anschaulich zu machen, schaut man sich am einfachsten eine Funktion und die zugehörige Ableitung-Funktion an.In Mathematica geht das über folgende Anweisungen:

f[x_] := x^3 - 9 x + 5;
Plot[{f[x], f'[x]}, {x, -4, 4}]

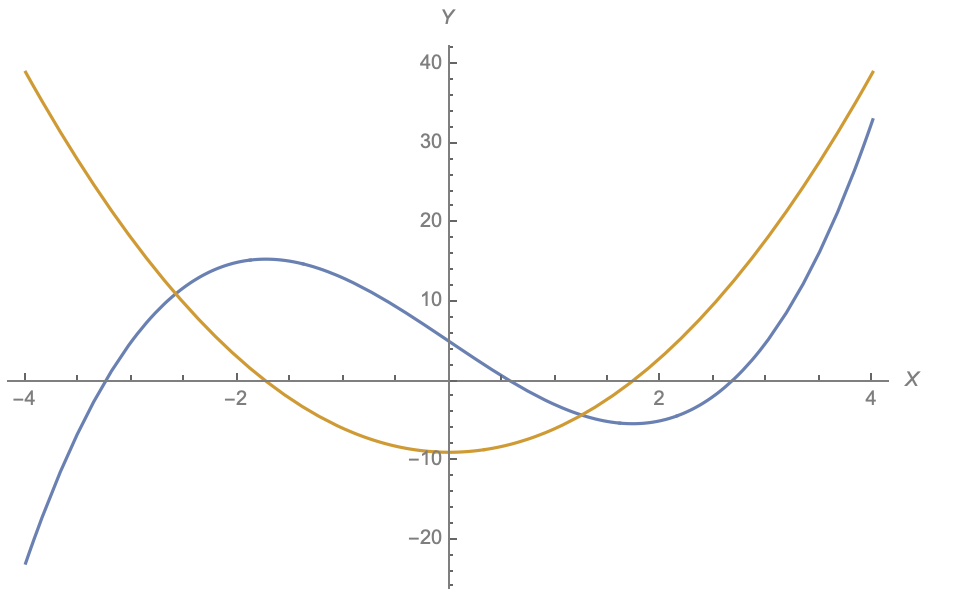
Wir sehen in der Graphik in Blau die Ursprungsfunktion und in Orange die Ableitungsfunktion. Dabei wird nun schon sehr deutlich, dass es nicht gerade intuitiv möglich ist, sich die Steigung (oder die Tangente mit der entsprechenden Steigung) auf dem blauen Graphen vorzustellen.

Relativ einfach kann man sich mit Mathematica nun erstmal eine Punkt-Menge auf dem Graphen vorstellen, an denen wir zur Veranschaulichung dann auch die Tangente anlegen werden. Nun aber zuerst zur Punkt-Menge.

Als erstes benötigen wir eine Liste mit Koordinaten der Punkte die wir auf dem Graphen darstellen möchten. Dazu nutzen wir folgenden Funktionsaufruf, der eine Liste über die Table-Funktion von x und zugehörigen f(x) Werten erzeugt:

Punktliste = Table[{x, f[x]}, {x, -4, 4, 0.25}]
Das ergibt dann folgende Liste:
{{-4., -23.}, {-3.75, -13.9844}, {-3.5, -6.375}, {-3.25, -0.078125}, \
{-3., 5.}, {-2.75, 8.95313}, {-2.5, 11.875}, {-2.25, 13.8594}, {-2., 
  15.}, {-1.75, 15.3906}, {-1.5, 15.125}, {-1.25, 14.2969}, {-1., 
  13.}, {-0.75, 11.3281}, {-0.5, 9.375}, {-0.25, 7.23438}, {0., 
  5.}, {0.25, 2.76563}, {0.5, 
  0.625}, {0.75, -1.32813}, {1., -3.}, {1.25, -4.29688}, {1.5, \
-5.125}, {1.75, -5.39063}, {2., -5.}, {2.25, -3.85938}, {2.5, \
-1.875}, {2.75, 1.04688}, {3., 5.}, {3.25, 10.0781}, {3.5, 
  16.375}, {3.75, 23.9844}, {4., 33.}}

Mit der Epilog-Funktion können diese Koordinaten dann als Punkte auf dem Graphen dargestellt werden:

Plot[f[x], {x, -4, 4}, 
 Epilog -> {PointSize[0.015], Hue[1], Map[Point, Punktliste]}]

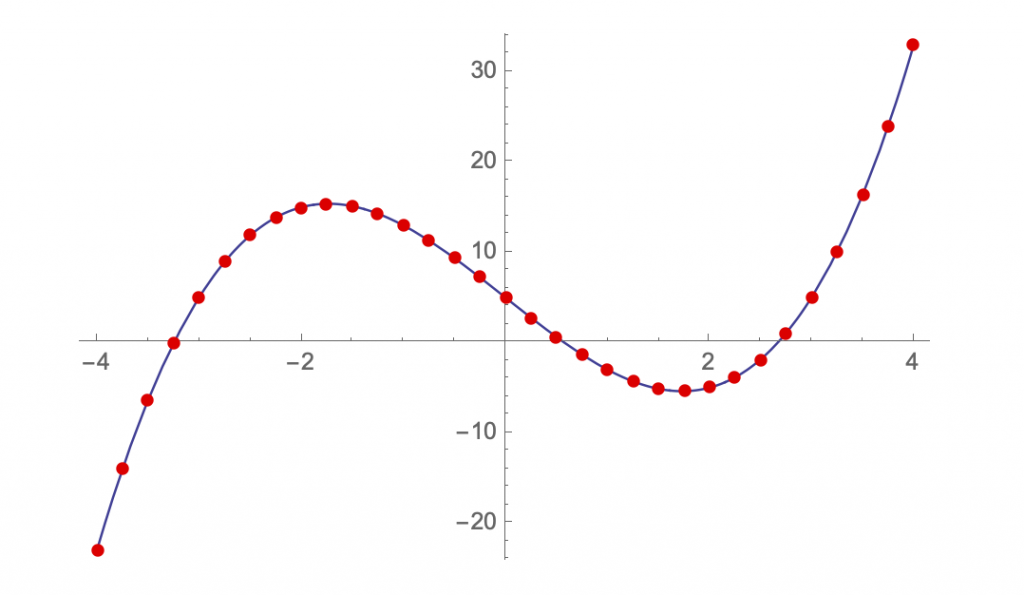
Nun stellt sich die Frage, wie man für alle diese Punkte eine Tangentengleichung bestimmt werden kann. Ausgangspunkt ist die bekannte Geradengleichung: . Wobei m die Steigung beschreibt und den y-Achsenabschnitt also den Abstand zur x-Achse bezeichnet.

Allgemein gilt für die Tangente an einem bestimmten Punkt eines Graphen der Funktion folgende Gleichung:

Mit Mathematica lässt sich das problem relativ einfach beschreiben. Man definiert die Ausgangsfunktion und die allgemeine Tangentengleichung und den Punkt und lässt sich das Ganze dann über die Plot-Funktion anzeigen.

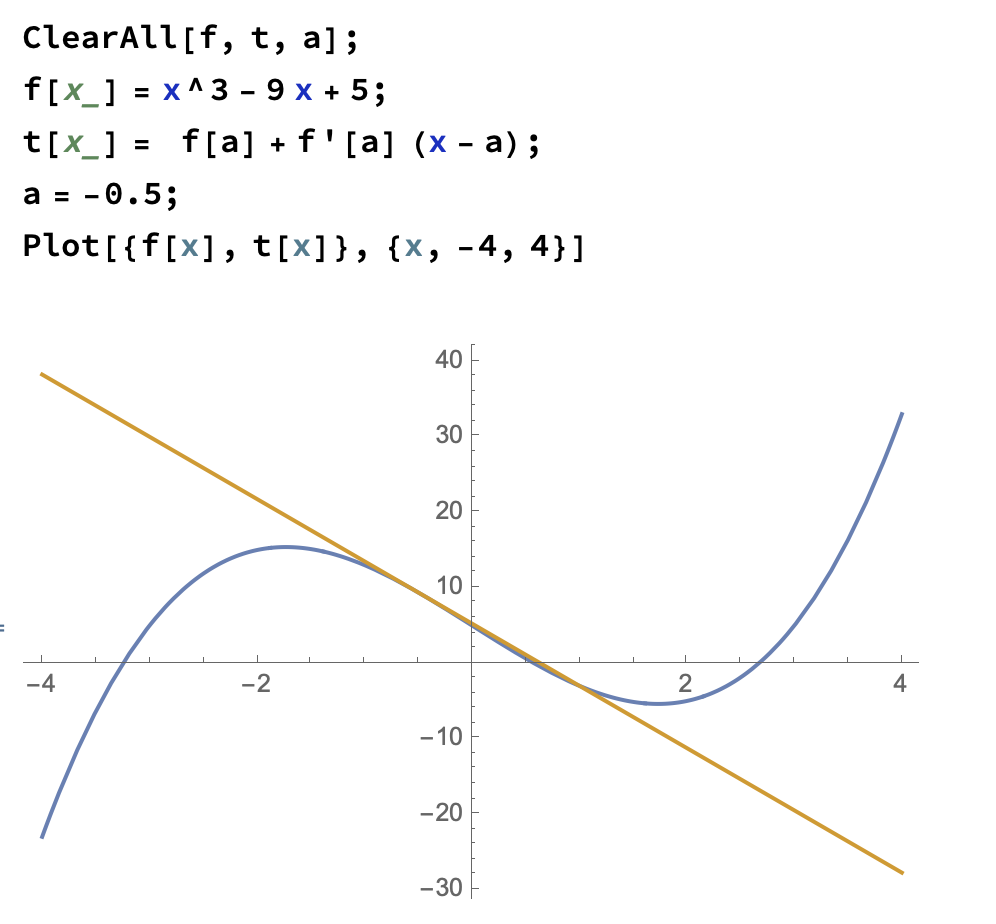
Möchte man dies nun für alle Punkte, mit einer kürzeren Tangente darstellen geht man wie folgt vor:

Für unsere Tangentengleichung kennen wir bereits die Steigung m, diese ergibt sich aus der Ableitung an einer bestimmten Position .

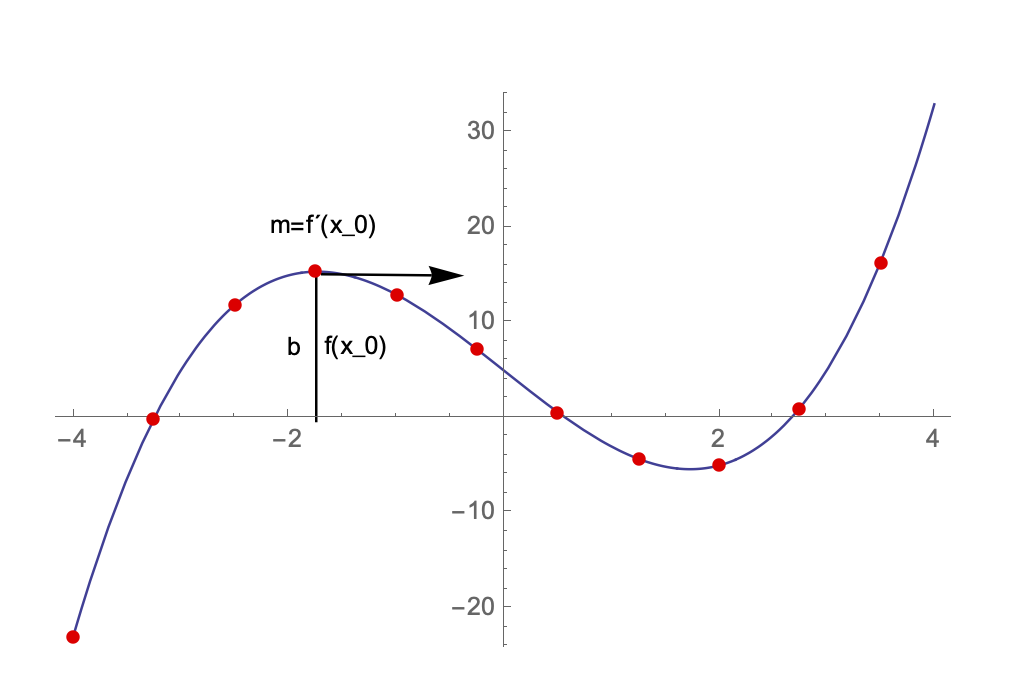
Der Parameter (Y-Achsen-Abschnitt) bestimmen wir über den Funktionswert des Graphen.

Punktliste1 = Table[{x, f[x]}, {x, -4, 4, 0.75}];
Plot[f[x], {x, -4, 4}, 
 Epilog -> {PointSize[0.015], Hue[1], Map[Point, Punktliste1]}]

Die nun fehlende Ziel-Koordinate bestimmen wir über folgende Überlegung: Ausgangs-Koordinate ist der Punkt und der zugehörige Funktionswert . Die Steigung des anzulegenden Pfeils entspricht der Ableitung damit lässt sich nun die Ziel-Koordinate berechnen in dem man auf der x-Achse ein Stück dazu addiert und y-Position über die Steigung und den y-Achsen-Abschnitt berechnet.

Tangentenliste = 
 Table[{{x, f[x]}, {(x + 0.25), f[x] + f'[x]*0.9}}, {x, -4, 4, 0.25}]

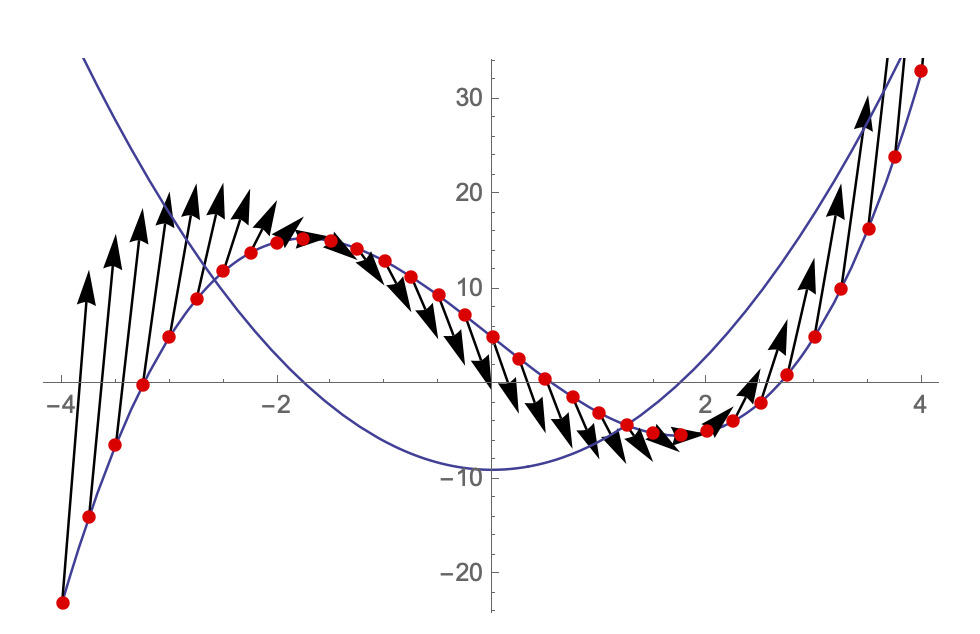
Mit diesen Informationen sind wir in der Lage die gewünschte Darstellung berechnen zu lassen:

Show[Plot[f[x], {x, -4, 4}, 
  Epilog -> {PointSize[0.015], Hue[1], Map[Point, Punktliste]}], 
 Graphics[Map[Arrow, Tangentenliste]], Plot[f'[x], {x, -4, 4}]]

Eine weitere Möglichkeit…mit Hilfe der Manipulate-Funktion

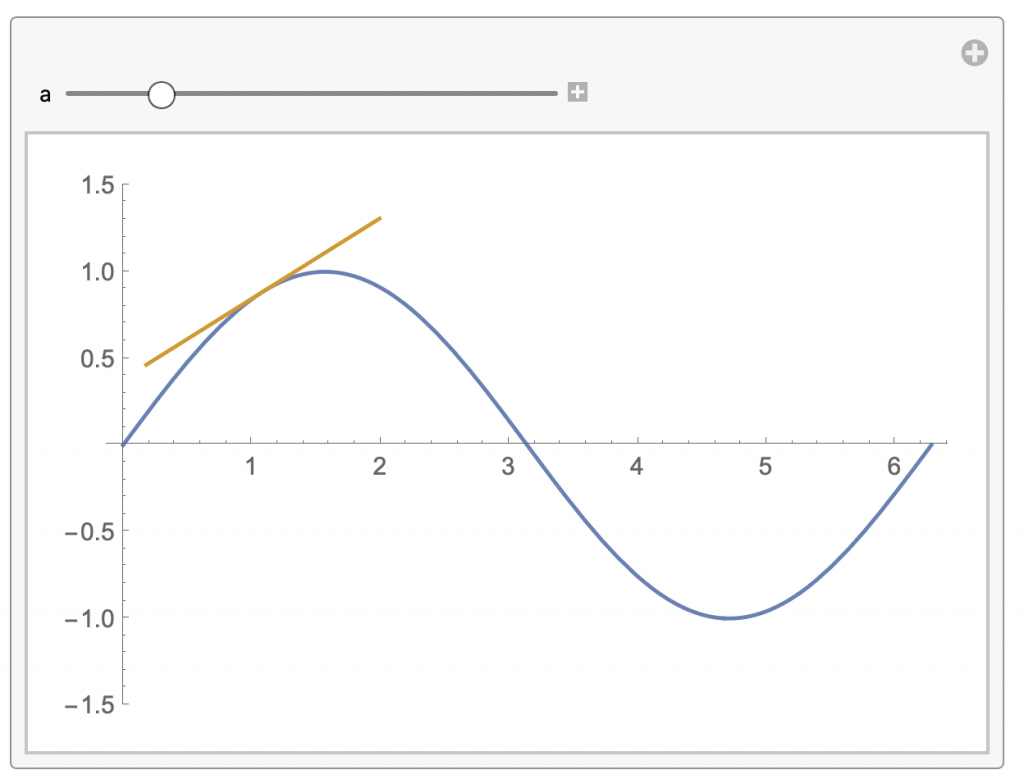
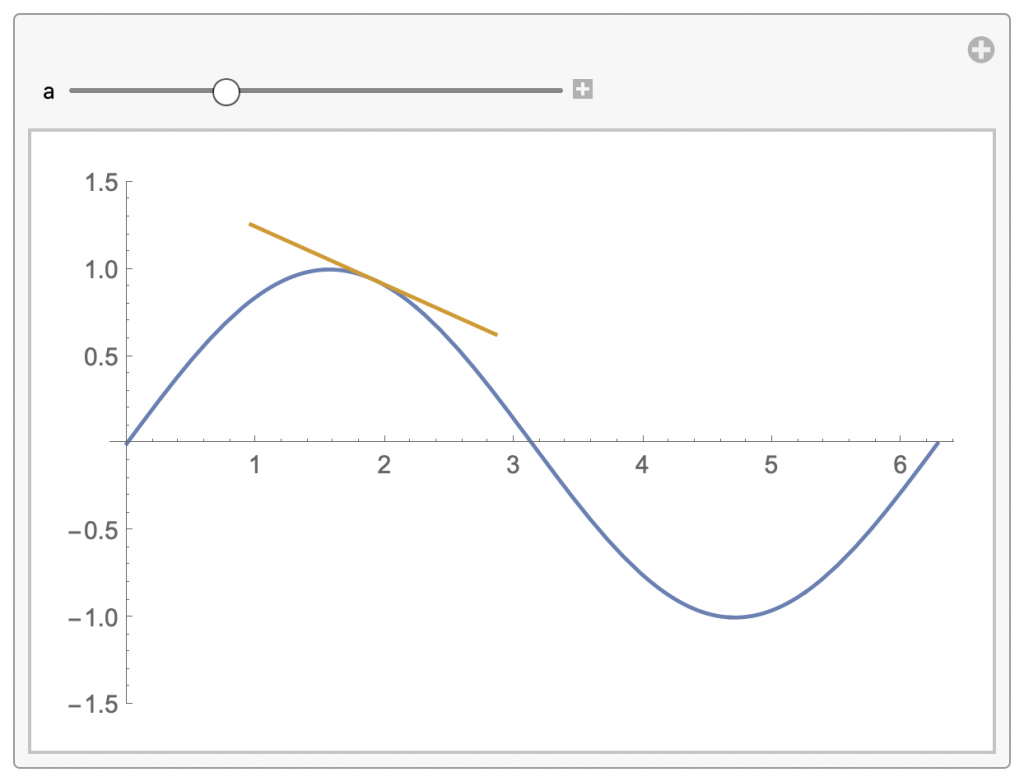
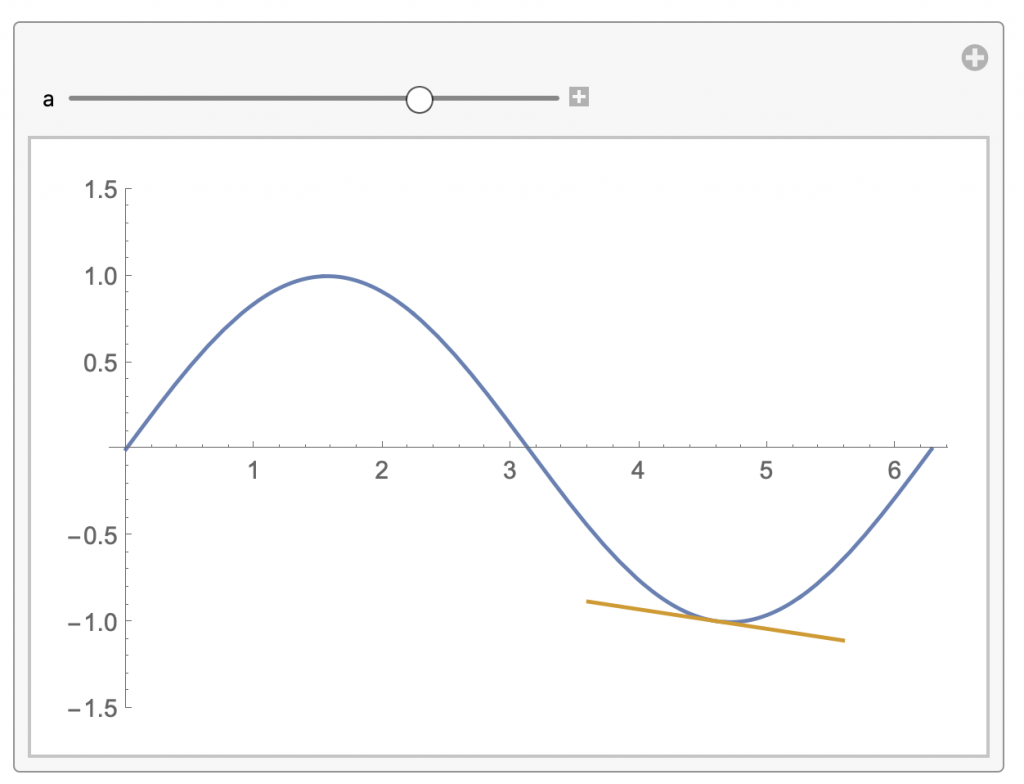
Manipulate bietet die Möglichkeit bestimmte Parameter zu verändern. Damit lassen sich insbesondere Zusammenhänge sehr einfach visualisieren. Im folgenden soll dies am Beispiel der Tangente sprich der Ableitung an der Sinus-Funktion vorgestellt werden:

f[x_] = Sin[x];
l[x_, a_] := 
 f[a] + f'[a] (x - a) /; 
  a - 1/(Sqrt[1 + (f'[a])^2]) <= x <= a + 1/(Sqrt[1 + (f'[a])^2])
Manipulate[
 Plot[{f[x], l[x, a]}, {x, 0, 2 \[Pi]}, PlotRange -> {-1.5, 1.5}], {a,
   0, 2 \[Pi]}]

Das ergibt dann in Abhängigkeit des Parameters a, der über die Manipulate-Funktion sowohl manuell als auch automatisch verändert werden kann, folgende Ausgabe:

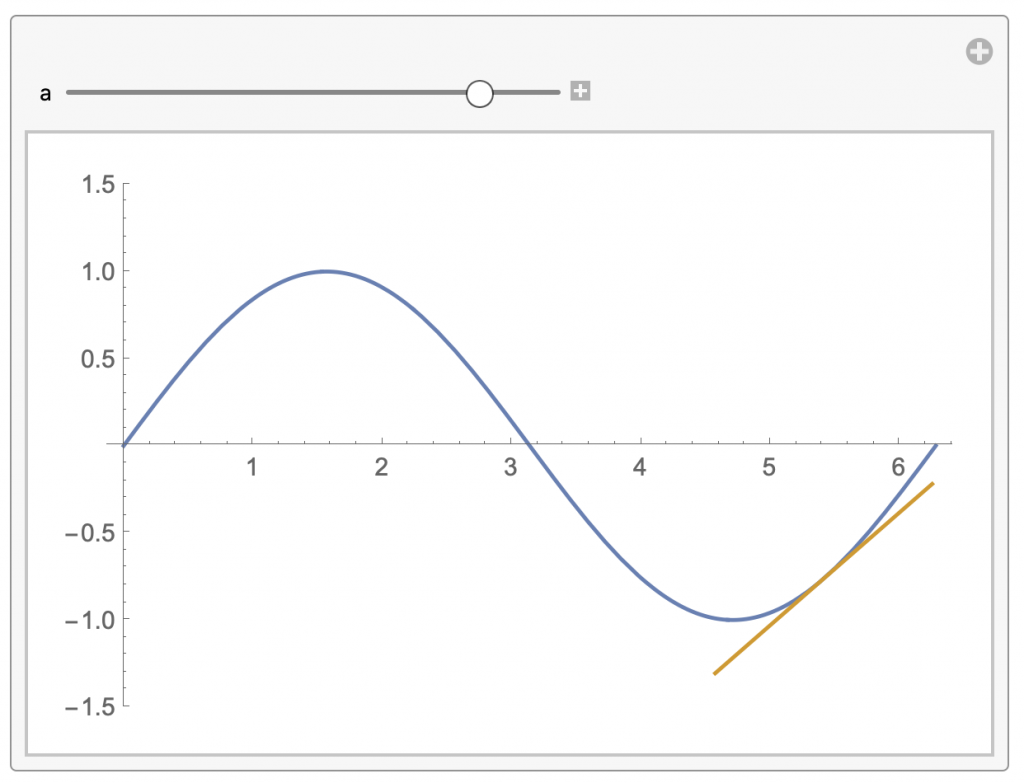
Damit dürfte es möglich sein, die Ableitung einer Funktion in 2 Dimensionen jedem Interessierten näher zu bringen. Hat man das einmal verstanden ist der Weg in die dritte Demission und zu den partiellen Ableitungen nicht mehr weit.